The initial height on each side was
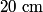 and and 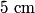 was added to one side, so the sum of the heights on the two sides must be was added to one side, so the sum of the heights on the two sides must be Also, the pressure 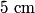 below the top of the left column must equal to the pressure at that same height on the right column. Therefore, the weight of the fluid above each of these locations must be the same below the top of the left column must equal to the pressure at that same height on the right column. Therefore, the weight of the fluid above each of these locations must be the same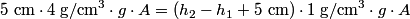 where 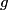 is the acceleration of gravity and is the acceleration of gravity and 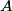 is the cross-sectional area of the tube. The above equation reduces to is the cross-sectional area of the tube. The above equation reduces to The solution to equations (1) and (2) is 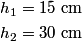 Therefore, the desired ratio is 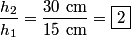 Therefore, answer (C) is correct. |